Sorting is a commonly used technique in the day to day life and almost each and every application sorts something or other according to the user requirements. Basically, Sorting is the process of arranging items systematically or say filtering the items in order to modify the existing items. Sorting is an important aspect with respect to Data Structures.
In this article, we will learn what is Merge Sorting and implement it programmatically using Python programming.
Also Read:- Implementing Queue Using A Linked List In Python Programming
Contents
Basics of Sorting
Sorting technically means to rearrange or modify something that could be a given list, in order to fetch the desired outcome of our choice. For example, we have 20 files that we want to sort in order of their date creation. Sorting is of two types.
- External Sorting – When all data that needs to be sorted cannot be placed in memory at a time, it is called external sorting. Eg: Merge Sort
- Internal Sorting – When all data is placed in memory, then sorting is called internal sorting.
What is Merge Sort?
Merge sort is a recursive & divide-and-conquer algorithm. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same or related type until these become simple enough to be solved directly. Based on the idea mentioned above, Merge Sort works.
In Merge Sort, an item let us consider a list or an array, is broken down into several sub-items until each subitem consists of a single element and merging those subitems in a manner that the result consists of the sorted items. If the list consists of more than one item, we split the list into two halves and recursively invoke a merge sort on both halves.
While comparing two halves for merging, the first element of both lists is taken into consideration. Once the two halves are sorted, the fundamental operation called the merge is performed. Merging is a process where two smaller sorted list are combined in a single sorted new list.
Important Things To Remember:
- Time Complexity: Time complexity of MergeSort is BigO(nLogn) in all 3 cases (worst, average and best) as Merge Sort always divides the array or list into two halves and take linear time to merge two halves.
- Auxiliary Space: O(n)
- Algorithmic Paradigm: Divide and Conquer
- Stable: Yes
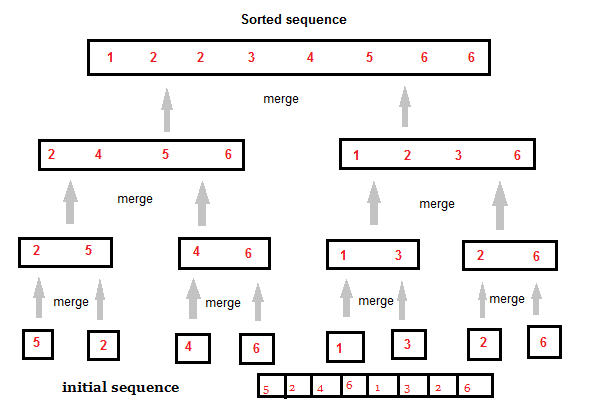
Diagrammatical Representation of Merge Sort
Observe the diagrammatical representation of implementing a Merge Sort in order to understand the concept better.
Initially, we might have an unsorted sequence and suppose our aim is to sort the given items in an ascending order so, the above approach is used in Merge Sort for sorting.
Also Read:- Implementation Of Binary Search Trees In Python (Part 1)
Algorithm for Merge Sort
Program in Python3
You can use any of the text editors to implement this program.
def merge_sort(arr):
# checking if array lenght is greter than 1 and this is the base case
if len(arr)>1:
# divide the given array in two half
mid = len(arr)/2
# creating two halves for the array
lefthalf = arr[:mid] # slice operation
righthalf = arr[mid:]
# call the merge_sort rescursively on the both halves
merge_sort(lefthalf)
merge_sort(righthalf)
# Making some index variable and initilize them to 0
i=0
j=0
k=0 # this will relate to the final array
# while loop for checking the mid point
while i < len(lefthalf) and j < len(righthalf):
# check if the lefthalf is less than the right
if lefthalf[i] < righthalf[j]:
# assign the kth element to lefthalf and increment the i index
arr[k]=lefthalf[i]
i=i+1
else:
# assign to the righthaflf and increment the j index
arr[k]=righthalf[j]
j=j+1
# then increment the k element
k=k+1
# check the lefthalf and continue the similary process
while i < len(lefthalf):
arr[k]=lefthalf[i]
i=i+1
k=k+1
# check the righthalf
while j < len(righthalf):
arr[k]=righthalf[j]
j=j+1
k=k+1
# putting some value in the array
arr = [11,2,5,4,7,6,8,1,23]
# call the merge_sort function
merge_sort(arr)
arr
In the above example, the mergesort is called recursively until the sorting satisfies the base condition. “i “and “j “ index basically checks that in which half we are i.e. whether it is lefthalf or righthalf. The three while loops are actually doing the merging of the sorted sublists. At the initial stage if the length of the list or array is 1 or 0 then no sorting is required as this is the base condition.
Challenge: Try to implement it dynamically instead of hard-coding the values in the array.
Hope you like the post. Do share and comment in the comments section below for your solution or a better approach. Thank you.