Implementation of Binary Search Trees in Python (Part 1)

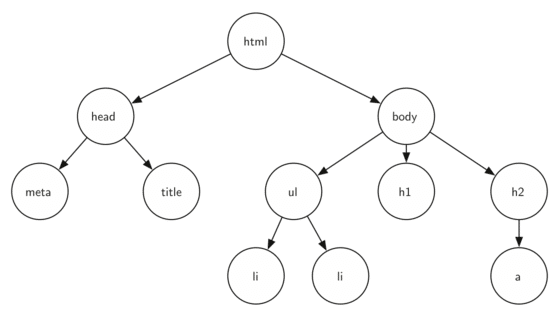
Tree is one of the non-linear data structures and perhaps one of the most rated and asked questions during the job interviews. In computer science, a tree is a widely used abstract data type (ADT)—or data structure that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes as shown below.

As a programmer, you should have a good command of these topics. So, this article is about what are Binary Search Trees and the code implementation of constructing a Binary Search Tree, Inserting items and then fetching those items in the Python programming language.

What are Binary Search Trees?

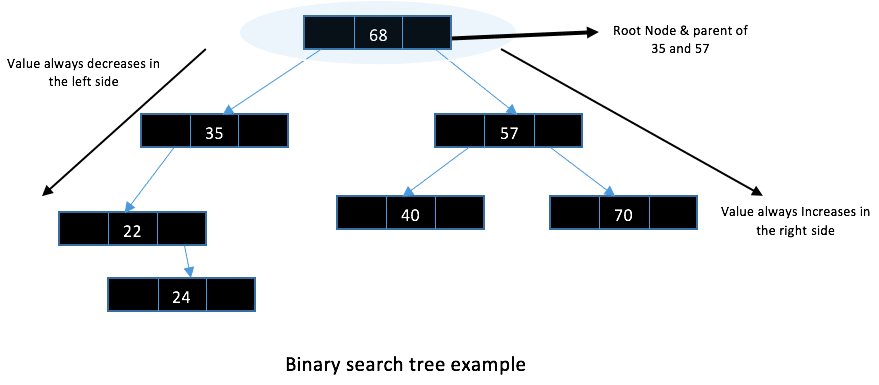
Binary Search trees are the special category of the tree that follows a predefined property of mapping the elements within the tree. This predefined property is that, in a Binary Search tree, all the elements that are smaller than the parent node are inserted at the left and all the elements greater than the parent node are inserted at the right as demonstrated in the figure below.

This property is called BST property and this guides us while inserting the new element in the Binary search trees as shown in the figure where we have inserted some elements in the tree. This BST property only refers to the direct parent, not the entire tree. for eg. 68 is the direct parent of 35 and 57 in the same way 57 is the direct parent for 40 and 70 and so on.

Node Structure in a tree or BST is shown in figure.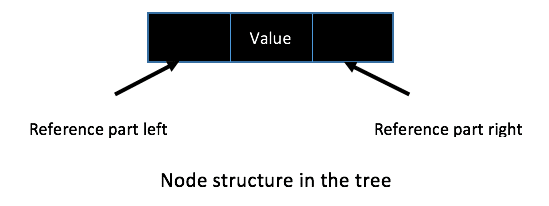68  inserted first in the tree is called Root Node. Suppose, if we want to insert 45, then where it should be inserted in the tree shown above?

Yes, it will be inserted as a right child of 40. This way we can insert elements into a BST.

Implementation through Code

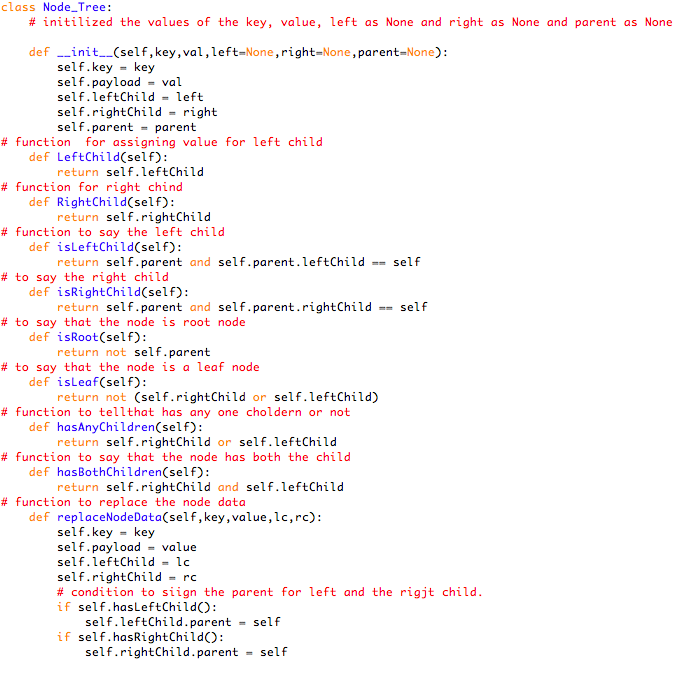
To implement BST, we will use the nodes and reference approach. Here, I have created two class one, BST_ Class and other  Node_Tree class.

Code for the Node_Tree class, you can implement this on any text editor.

This class has the basic functionality for managing the nodes of the tree i.e right child, left child, replace data.

Now, our BST_Class will be using this Tree_Node class for the operations on the Binary search trees. The basic structure of the BST_Class tree will look like this.

Code for various operations in the Binary Search Tree

1.  We have a check_key function and the _putitem function. Check_key checks if we have any key or not, if not we assign that as the root node and then check for the other key using the _putitem method and follow the bst property to insert the elements by the recessive calling of the _putitem method. Keep writing this code in the BST_Class tree method after __len__(self) method.

The functions will look like this.

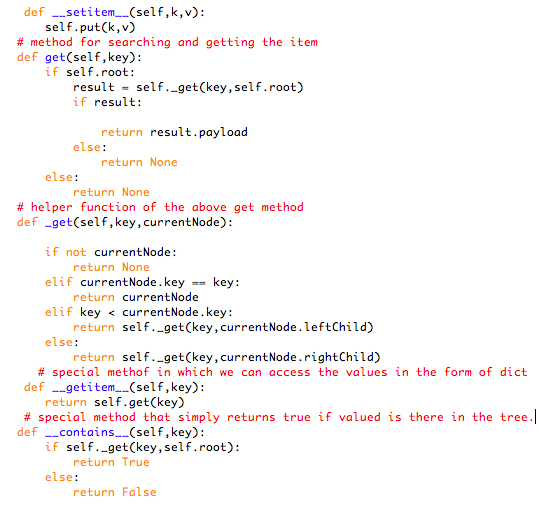
These codes are using the check_Key method to put the new elements in our Binary Search Tree. Once the tree is constructed then we need to retrieve the data for that we have the get method coded below.

The get method simply searches the in the tree until it gets to a non-matching leaf node or a matching node and when the value is found then it stores that value in the payload.

The above codes were for making a tree, inserting item and then search any key from the tree. Now we need to have the deletion operation. This operation is a little trick and challenging to implement. We will discuss the deletion method separately in the next article.